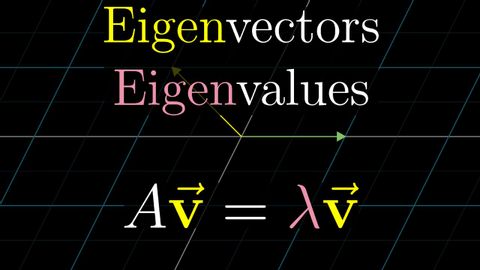
Subtitles & vocabulary
00
Save
Video vocabulary
stretch
US /strɛtʃ/
・
UK /stretʃ/
- Verb (Transitive/Intransitive)
- To make your arm, leg muscles long to ease them
- To make something bigger by pulling on it
- Noun
- Making arm, leg muscles longer to ease them
- A consecutive row of things
A2TOEIC
More expression
US /ɪkˈsprɛʃən/
・
UK /ɪk'spreʃn/
- Noun (Countable/Uncountable)
- Act of making your thoughts and feelings known
- Group of words that have a specific meaning
A2TOEIC
More scale
US /skel/
・
UK /skeɪl/
- Noun (Countable/Uncountable)
- Size, level, or amount when compared
- Small hard plates that cover the body of fish
- Verb (Transitive/Intransitive)
- To change the size of but keep the proportions
- To climb something large (e.g. a mountain)
A2TOEIC
More spot
US /spɑt/
・
UK /spɒt/
- Noun
- A certain place or area
- A difficult time; awkward situation
- Transitive Verb
- To see someone or something by chance
A2TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
