Subtitles & vocabulary
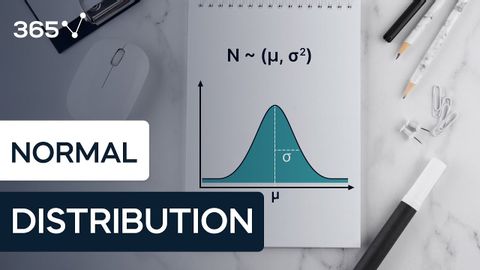
The Normal Distribution
00
林宜悉 posted on 2020/03/09Save
Video vocabulary
perspective
US /pɚˈspɛktɪv/
・
UK /pə'spektɪv/
- Noun (Countable/Uncountable)
- Artistic method of creating a sense of distance
- Ability to understand what is important in life
B1TOEIC
More recognize
US /ˈrek.əɡ.naɪz/
・
UK /ˈrek.əɡ.naɪz/
- Transitive Verb
- To accept the truth or reality of something
- To consider something as important or special
A2TOEIC
More term
US /tɚm/
・
UK /tɜ:m/
- Noun (Countable/Uncountable)
- Conditions applying to an agreement, contract
- Length of time something is expected to happen
- Transitive Verb
- To call; give a name to
A1TOEIC
More determine
US /dɪˈtɚmɪn/
・
UK /dɪ'tɜ:mɪn/
- Transitive Verb
- To control exactly how something will be or act
- To establish the facts about; discover
A2TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
