Subtitles & vocabulary
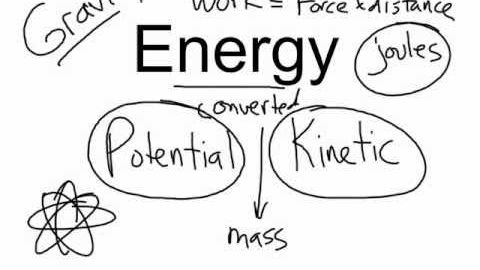
Potential and Kinetic Energy
00
Cheng-Hong Liu posted on 2015/02/18Save
Video vocabulary
potential
US /pəˈtɛnʃəl/
・
UK /pəˈtenʃl/
- Adjective
- Capable of happening or becoming reality
- Having or showing the capacity to develop into something in the future.
- Uncountable Noun
- someone's or something's ability to develop, achieve, or succeed
A2TOEIC
More figure
US /ˈfɪɡjɚ/
・
UK /ˈfiɡə/
- Verb (Transitive/Intransitive)
- To appear in a game, play or event
- To calculate how much something will cost
- Noun
- Your body shape
- Numbers in a calculation
A1TOEIC
More significant
US /sɪɡˈnɪfɪkənt/
・
UK /sɪgˈnɪfɪkənt/
- Adjective
- Large enough to be noticed or have an effect
- Having meaning; important; noticeable
A2TOEIC
More throw
US /θroʊ/
・
UK /θrəʊ/
- Transitive Verb
- To use your arm to make something fly in the air
- To move part of your body suddenly and forcefully
- Noun (Countable/Uncountable)
- Arm movement to make a thing fly through the air
- Loose cloth or blanket (usually over a chair)
A1
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
