Subtitles & vocabulary
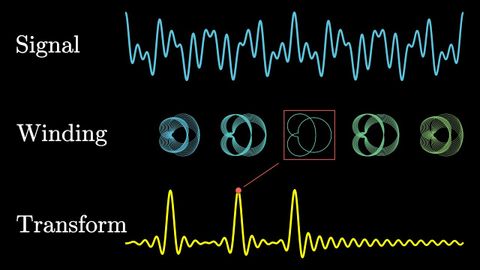
But what is the Fourier Transform? A visual introduction.
00
Sujuku posted on 2022/11/16Save
Video vocabulary
context
US /ˈkɑnˌtɛkst/
・
UK /ˈkɒntekst/
- Noun (Countable/Uncountable)
- Set of facts surrounding a person or event
- The circumstances that form the setting for an event, statement, or idea, and in terms of which it can be fully understood and assessed.
A2
More expression
US /ɪkˈsprɛʃən/
・
UK /ɪk'spreʃn/
- Noun (Countable/Uncountable)
- Act of making your thoughts and feelings known
- Group of words that have a specific meaning
A2TOEIC
More scale
US /skel/
・
UK /skeɪl/
- Noun (Countable/Uncountable)
- Size, level, or amount when compared
- Small hard plates that cover the body of fish
- Verb (Transitive/Intransitive)
- To change the size of but keep the proportions
- To climb something large (e.g. a mountain)
A2TOEIC
More negative
US /ˈnɛɡətɪv/
・
UK /'neɡətɪv/
- Noun
- The opposite to a positive electrical charge
- In grammar, containing words such as 'no' or 'not'
- Adjective
- Being harmful, unwanted or unhelpful
- In mathematics, being less than zero
A2
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
