Subtitles & vocabulary
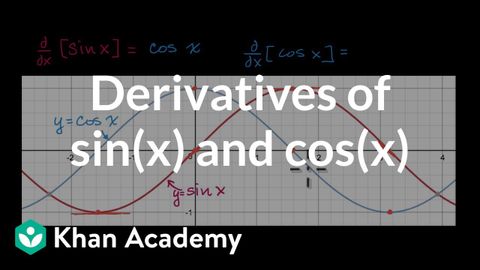
Derivatives of sin(x) and cos(x) | Derivative rules | AP Calculus AB | Khan Academy
00
yukang920108 posted on 2022/07/12Save
Video vocabulary
positive
US /ˈpɑzɪtɪv/
・
UK /ˈpɒzətɪv/
- Adjective
- Showing agreement or support for something
- Being sure about something; knowing the truth
- Noun
- A photograph in which light areas are light and dark areas are dark
A2
More negative
US /ˈnɛɡətɪv/
・
UK /'neɡətɪv/
- Noun
- The opposite to a positive electrical charge
- In grammar, containing words such as 'no' or 'not'
- Adjective
- Being harmful, unwanted or unhelpful
- In mathematics, being less than zero
A2
More intuitive
US /ɪnˈtuɪtɪv, -ˈtju-/
・
UK /ɪnˈtju:ɪtɪv/
- Adjective
- Able to understand by feeling rather than fact
- Easy to use and understand.
B2
More sense
US /sɛns/
・
UK /sens/
- Noun (Countable/Uncountable)
- Certain mental feeling or emotion
- Normal or clear state of mind
- Verb (Transitive/Intransitive)
- To perceive using sight, sound, taste touch etc.
- To recognize the presence of something
A1TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
