Subtitles & vocabulary
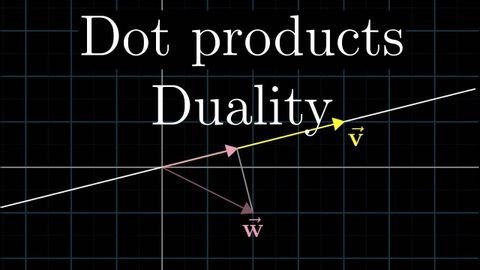
Dot products and duality | Essence of linear algebra, chapter 9
00
tai posted on 2021/02/16Save
Video vocabulary
stuff
US /stʌf/
・
UK /stʌf/
- Uncountable Noun
- Generic description for things, materials, objects
- Transitive Verb
- To push material inside something, with force
B1
More process
US /ˈprɑsˌɛs, ˈproˌsɛs/
・
UK /prə'ses/
- Transitive Verb
- To organize and use data in a computer
- To deal with official forms in the way required
- Noun (Countable/Uncountable)
- Dealing with official forms in the way required
- Set of changes that occur slowly and naturally
A2TOEIC
More constant
US /ˈkɑnstənt/
・
UK /'kɒnstənt/
- Adjective
- Happening frequently or without pause
- Remaining the same over time or not changing.
- Noun
- Thing that happens always or at a regular rate
- A physical quantity that is believed to have a fixed value and is used in calculations.
A2TOEIC
More matter
US /ˈmætɚ/
・
UK /'mætə(r)/
- Intransitive Verb
- To be of great importance; to count
- Uncountable Noun
- Material all things are made of that fills space
A1TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
