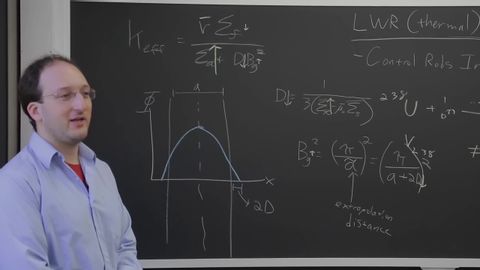
Subtitles & vocabulary
00
Save
Video vocabulary
critical
US /ˈkrɪtɪkəl/
・
UK /ˈkrɪtɪkl/
- Adjective
- Making a negative judgment of something
- Being important or serious; vital; dangerous
A2
More material
US /məˈtɪriəl/
・
UK /məˈtɪəriəl/
- Noun (Countable/Uncountable)
- Cloth; fabric
- Supplies or data needed to do a certain thing
- Adjective
- Relevant; (of evidence) important or significant
- Belonging to the world of physical things
A2
More period
US /ˈpɪriəd/
・
UK /ˈpɪəriəd/
- Noun (Countable/Uncountable)
- Set amount of time during which events take place
- A way to emphasize what you will say
A1TOEIC
More term
US /tɚm/
・
UK /tɜ:m/
- Noun (Countable/Uncountable)
- Conditions applying to an agreement, contract
- Length of time something is expected to happen
- Transitive Verb
- To call; give a name to
A1TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
