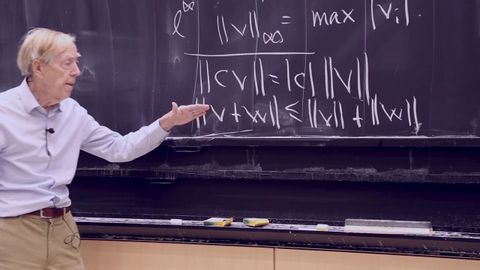
Subtitles & vocabulary
00
Save
Video vocabulary
bunch
US /bʌntʃ/
・
UK /bʌntʃ/
- Noun (Countable/Uncountable)
- A group of things of the same kind
- A group of people.
- Transitive Verb
- To group people or things closely together
B1
More average
US /ˈævərɪdʒ, ˈævrɪdʒ/
・
UK /'ævərɪdʒ/
- Noun (Countable/Uncountable)
- Total of numbers divided by the number of items
- Transitive Verb
- To add numbers then divide by the number of items
A2TOEIC
More negative
US /ˈnɛɡətɪv/
・
UK /'neɡətɪv/
- Noun
- The opposite to a positive electrical charge
- In grammar, containing words such as 'no' or 'not'
- Adjective
- Being harmful, unwanted or unhelpful
- In mathematics, being less than zero
A2
More audience
US /ˈɔdiəns/
・
UK /ˈɔ:diəns/
- Noun (Countable/Uncountable)
- Group of people attending a play, movie etc.
A2TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
