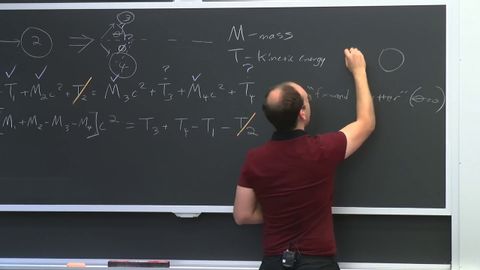
Subtitles & vocabulary
6. The Q-Equation — The Most General Nuclear Reaction
00
林宜悉 posted on 2020/03/29Save
Video vocabulary
stuff
US /stʌf/
・
UK /stʌf/
- Uncountable Noun
- Generic description for things, materials, objects
- Transitive Verb
- To push material inside something, with force
B1
More stick
US /stɪk/
・
UK /stɪk/
- Verb (Transitive/Intransitive)
- To push a sharp or pointed object into something
- To join together using glue or paste
- Countable Noun
- Long thin piece of wood from a tree
A2
More term
US /tɚm/
・
UK /tɜ:m/
- Noun (Countable/Uncountable)
- Conditions applying to an agreement, contract
- Length of time something is expected to happen
- Transitive Verb
- To call; give a name to
A1TOEIC
More intuitive
US /ɪnˈtuɪtɪv, -ˈtju-/
・
UK /ɪnˈtju:ɪtɪv/
- Adjective
- Able to understand by feeling rather than fact
- Easy to use and understand.
B2
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
