Subtitles & vocabulary
Markov chains (Language of Coins: 11/16)
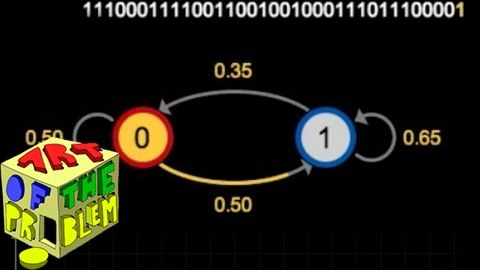
00
Lypan posted on 2015/10/18Save
Video vocabulary
state
US /stet/
・
UK /steɪt/
- Noun (Countable/Uncountable)
- Region within a country, with its own government
- Situation or condition something is in
- Adjective
- Concerning region within a country
A1TOEIC
More claim
US /klem/
・
UK /kleɪm/
- Noun (Countable/Uncountable)
- To say that something is true, often without proof.
- A statement that something is true.
- Transitive Verb
- To demand or ask for something that you believe is rightfully yours.
- To take or cause the loss of (e.g., a life, property).
A2
More light
US /laɪt/
・
UK /laɪt/
- Transitive Verb
- To cause something to burn; put a burning match to
- To provide a way to see ahead
- Adjective
- Being bright making it easy to see; not dark
- Being pale and lacking darkness of color
A1
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
