Subtitles & vocabulary
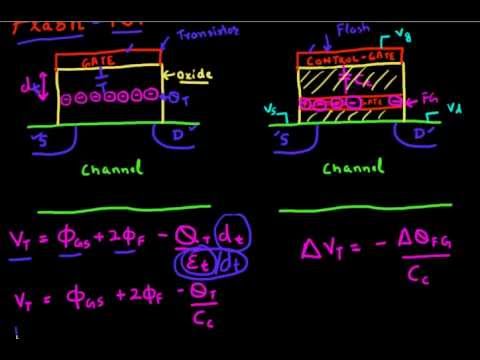
Baics of Flash Memory Operation: Part 1
00
陳震寰 posted on 2015/05/01Save
Video vocabulary
potential
US /pəˈtɛnʃəl/
・
UK /pəˈtenʃl/
- Adjective
- Capable of happening or becoming reality
- Having or showing the capacity to develop into something in the future.
- Uncountable Noun
- someone's or something's ability to develop, achieve, or succeed
A2TOEIC
More essentially
US /ɪˈsenʃəli/
・
UK /ɪˈsenʃəli/
- Adverb
- Basically; (said when stating the basic facts)
- Used to emphasize the basic truth or fact of a situation.
A2
More couple
US /ˈkʌpəl/
・
UK /'kʌpl/
- Transitive Verb
- To join something to something else
- (Two animals) to engage in sexual relations
- Noun (Countable/Uncountable)
- Two people in a romantic relationship
- Two of something; two people; a pair
A2
More charge
US /tʃɑrdʒ/
・
UK /tʃɑ:dʒ/
- Verb (Transitive/Intransitive)
- To run quickly toward someone to attack them
- To ask for money as a price for a service or goods
- Noun (Countable/Uncountable)
- An attack by running quickly toward someone
- A price for a service or goods
A2
More Use Energy
Unlock Vocabulary
Unlock pronunciation, explanations, and filters
