Subtitles & vocabulary
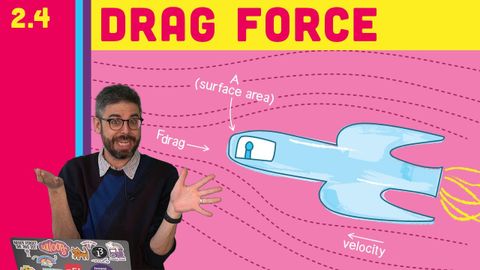
2.4 Drag Force - The Nature of Code
00
林宜悉 posted on 2020/04/15Save
Video vocabulary
assume
US /əˈsum/
・
UK /ə'sju:m/
- Transitive Verb
- To act in a false manner to mislead others
- To believe, based on the evidence; suppose
A2TOEIC
More absolutely
US /ˈæbsəˌlutli, ˌæbsəˈlutli/
・
UK /ˈæbsəlu:tli/
- Adverb
- Completely; totally; very
- Considered independently and without relation to other things; viewed abstractly; as, quantity absolutely considered.
A2
More constant
US /ˈkɑnstənt/
・
UK /'kɒnstənt/
- Adjective
- Happening frequently or without pause
- Remaining the same over time or not changing.
- Noun
- Thing that happens always or at a regular rate
- A physical quantity that is believed to have a fixed value and is used in calculations.
A2TOEIC
More demonstrate
US /ˈdɛmənˌstret/
・
UK /'demənstreɪt/
- Verb (Transitive/Intransitive)
- To display a feeling or ability openly
- To protest about something often as a group
A2TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
