Subtitles & vocabulary
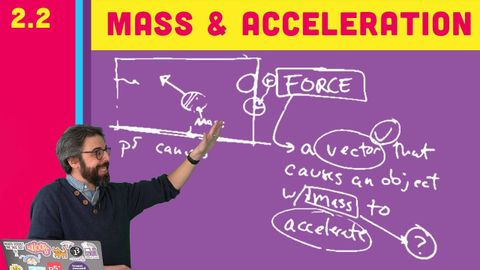
2.2 Mass and Acceleration - The Nature of Code
00
林宜悉 posted on 2020/04/06Save
Video vocabulary
ultimately
US /ˈʌltəmɪtli/
・
UK /ˈʌltɪmətli/
- Adverb
- Done or considered as the final and most important
- Fundamentally; at the most basic level.
B1TOEIC
More demonstrate
US /ˈdɛmənˌstret/
・
UK /'demənstreɪt/
- Verb (Transitive/Intransitive)
- To display a feeling or ability openly
- To protest about something often as a group
A2TOEIC
More scale
US /skel/
・
UK /skeɪl/
- Noun (Countable/Uncountable)
- Size, level, or amount when compared
- Small hard plates that cover the body of fish
- Verb (Transitive/Intransitive)
- To change the size of but keep the proportions
- To climb something large (e.g. a mountain)
A2TOEIC
More arbitrary
US /ˈɑrbɪˌtrɛri/
・
UK /ˈɑ:bitrəri/
- Adjective
- (Of decisions) unsupported; without any evidence
- Based on random choice or personal whim, rather than any reason or system.
B1TOEIC
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
