Subtitles & vocabulary
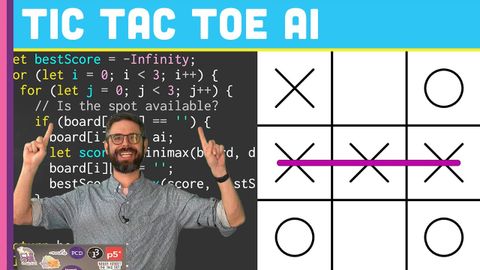
Coding Challenge 154: Tic Tac Toe AI with Minimax Algorithm
00
林宜悉 posted on 2020/03/27Save
Video vocabulary
ultimately
US /ˈʌltəmɪtli/
・
UK /ˈʌltɪmətli/
- Adverb
- Done or considered as the final and most important
- Fundamentally; at the most basic level.
B1TOEIC
More scenario
US /səˈner.i.oʊ/
・
UK /sɪˈnɑː.ri.əʊ/
- Noun
- An imagined sequence of events in a plan/project
B1
More figure
US /ˈfɪɡjɚ/
・
UK /ˈfiɡə/
- Verb (Transitive/Intransitive)
- To appear in a game, play or event
- To calculate how much something will cost
- Noun
- Your body shape
- Numbers in a calculation
A1TOEIC
More negative
US /ˈnɛɡətɪv/
・
UK /'neɡətɪv/
- Noun
- The opposite to a positive electrical charge
- In grammar, containing words such as 'no' or 'not'
- Adjective
- Being harmful, unwanted or unhelpful
- In mathematics, being less than zero
A2
More Use Energy
Unlock All Vocabulary
Unlock pronunciation, explanations, and filters
